Esta deslocação do vértice determina que as arestas laterais da pirâmide só serão visíveis, na projecção horizontal, quando o vértice se situar acima do plano da base. Estas arestas serão invisíveis nesta projecção se o plano da base tiver maior cota do que o vértice:
Observação: depois de determinadas as projecções do ponto O, do plano da base e da circunferência circunscrita ao hexágono, há que determinar A1, nela contido, e só depois o hexágono em verdadeira grandeza, a partir do qual se determina a respectiva projecção frontal.
O vértice V deverá pertencer a um segmento de recta correspondente à projecção frontal da recta vertical que contém o eixo da pirâmide.
A determinação do traçado adequado para a visibilidade das arestas laterais na projecção horizontal, decorre da representação de uma semi-recta auxiliar que intersecta uma das arestas laterais da pirâmide apenas quando esta se situa acima do plano da base, permitindo definir os pontos X e Y, que, por sua vez, possibilitam-nos a construção de 12 segmentos de recta correspondentes à representação das arestas laterais visíveis, em projecção horizontal, com um traçado expressivo.
Neste desenho, estes elementos foram desenhados a verde:
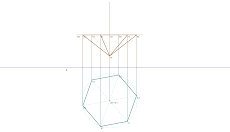
Para quem quiser avançar um pouco mais neste tipo de representações, utilizando os traçados adequados e convenientemente expressivos de que o software utilizado não dispõe, poderá, aplicando um raciocínio idêntico ao do desenho anterior (para a determinação dos pontos auxiliares Y e Z), e mediante um pouco mais de trabalho, realizar a seguinte representação:
Bom trabalho!


















Sem comentários:
Enviar um comentário